DATA 3.1 Professional - Was eine Auswertung ausmacht

Wie sagte doch gleich unser Professor: „Nun laßt uns die gemessenen Daten auswerten“. Da ich mein Studium der Physik längst hinter mir gelassen hatte und als wissenschaftlicher Mitarbeiter an der Uni arbeitete, wußte ich natürlich sofort, was er meinte: Zuerst mußten die Daten aufbereitet werden, d.h. sie wurden kalibriert, substituiert oder transformiert. Danach suchte man nach einer Approximations- bzw. Interpolations-Kurve, die den funktionalen Zusammenhang am besten wiedergab. Von dieser wurde anschließend das Integral oder Differential gebildet. Auch eine Skizze des Versuchsaufbaus durfte auf dem Diagramm nicht fehlen. Für eine Veröffentlichung mußte die Auswertung dann noch in bester Qualität zu Papier gebracht werden. Doch das alles per Hand? Ja, wenn es da nicht...

Aber zuerst einmal der Reihe nach: Was versteht man überhaupt unter einem Auswerte-Programm? Am besten erklärt man den Unterschied zu einem Business-Programm (z.B. K-Graph, Sci Graph) und einer Tabellenkalkulation, wobei die heutigen Tabellenkalkulationen bereits einen Business-Teil (Grafikteil) beinhalten. Business-Programme stellen vorgegebene (Meß-)Daten grafisch in ansprechender Form dar, d.h. die Grafik muß nachher in bester Qualität auf Papier präsentiert werden, daher auch Präsentationsgrafik. Werden die Daten interpoliert oder approximiert (was meist nur in beschränktem Umfang möglich ist), so werden die Kurven zwar auf dem Bildschirm dargestellt, sie liegen aber nicht, wie bei einem Auswerte-Programm, in Weltkoordinaten vor. Ein in Weltkoordinaten arbeitendes Programm hält ständig mehrere Kurven (Graphdaten), Meßreihen, Glättungsparameter usw. als REAL-Werte (bei DATA mit 19 Stellen) im Speicher, so daß z.B. mathematische Manipulationen auch im Nachhinein noch möglich sind. Ein Auswerte-Programm sollte die Möglichkeiten eines Business-Programms (z.B. Vektor-Grafik, publikationsreife Grafik usw.) und die einer Tabellenkalkulation (z.B. Datenmanipulation. mathematische Berechnungen usw.) miteinander verbinden und zusätzlich in Weltkoordinaten arbeiten.

Die neue Version

Das Programm DATA 3.1 geht dabei über diese Forderungen weit hinaus und stellt damit eines der komplexesten Werkzeuge auf dem Atari ST/TT dar. DATA wurde bereits erstmalig vor drei Jahren in der Version 1.0 getestet [1]. Deshalb beziehe ich mich im folgenden auf die wesentlichen Neuerungen der DATA-Version 3.1. Das Programm macht auf Anhieb einen übersichtlichen Eindruck. Dazu trägt vor allem die GEM-Benutzeroberfläche (eigener Desktop) mit Icons, Windows. Pull-Down-/Pull-Up-Menüs und interaktiven Grafiken bei (läuft auch unter MultiGEM). Accessories können während des Programms benutzt werden. Ein integrierter Vektor-Grafik-Editor befindet sich in einem eigenen Bearbeitungsfenster. DATA 3.1 stellt somit eine „reinrassige“ GEM-Anwendung dar. Das Programm läuft sowohl auf einem Großbildschirm als auch auf dem TT, wobei auf dem TT die Darstellung in hoher und in mittlerer (Färb-) Auflösung möglich ist. Die Auswertungen können vollkommen farbig gestaltet werden. Die Farbe macht besonders im Umgang mit einem Plotter Sinn. Die grafische Ausgabe erfolgt über GDOS-Device-Treiber in der höchstmöglichen Auflösung der jeweiligen Geräte (z.B. HP Laseijet, NEC P6+, HPGL-Plotter usw.). Die wichtigsten Geräte befinden sich als Icon auf dem Desktop. Will man eine Grafik ausdrucken. zieht man einfach das Auswerte- auf das Drucker-Icon. Vorteilhaft ist. daß man mehrere Geräte vom DATA-Desktop ansprechen kann. Genauso kann man eine Grafik als GEM-Meta-file abspeichern oder das Klemmbrett (Clipboard) benutzen, indem man z.B. das Vektor-Grafik- auf das Metafile-Icon zieht. Das Prinzip von Ziehen und Fallen lassen (Drag and Drop) wurde auch sonst konsequent angewandt. Nach meiner Erfahrung ist DATA eines der wenigen Programme, die GEM-Metafiles korrekt erzeugen. Lädt man z.B. das Metafile in den Timeworks-Publisher ein, hat man praktisch eine Eins-zu-Eins-Abbildung vorliegen. Die meisten Programme, die von sich behaupten, GEM-Metafiles korrekt zu schreiben, lassen entweder den Text vermissen, oder die Attribute, die Linienformen usw. stimmen nicht überein.

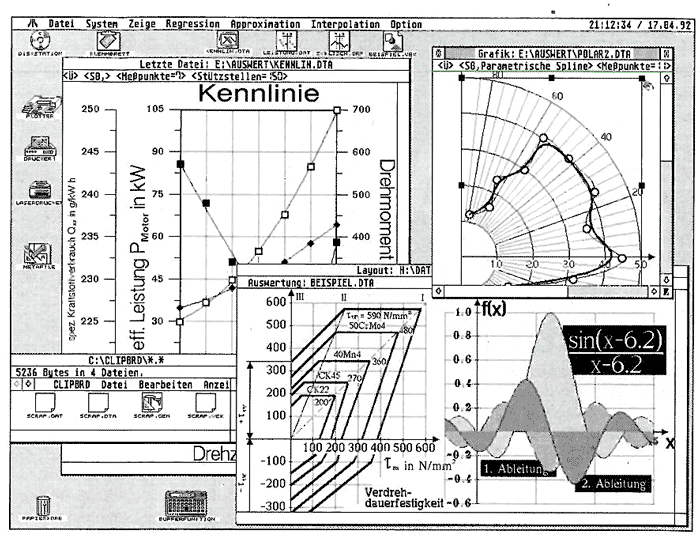
Die Pull-Down-Menü-Einträge gliedern sich auf in Dateioperationen, Koordinatensystemauswahl, Darstellungsarten (Funktions-Plot, Balkengrafiken etc.), Regressions-. Approximations- und Interpolations-Algorithmen bis hin zu den Optionsmenüs (Bild 2). Trotzdem finden nicht alle Funktionen des Programms darin Platz. Die Menüs Array, Seite, Grafik, Makro und Device befinden sich als sog. Pull-Up-Menüs auf dem Desktop in einer gemeinsamen verschiebbaren Box (Bild 3). Eine Beschreibung der einzelnen Möglichkeiten würde jedoch den Rahmen dieses Tests sprengen.

Das Konzept

DATA läßt sich in drei Bearbeitungsebenen einteilen:

• Auswertungsebene
• Vektor-Grafik-Ebene
• Layout-Ebene

Die einzelnen Ebenen befinden sich in getrennten Fenstern. Man kann einfach in eine andere Ebene wechseln, indem man das entsprechende Fenster anklickt.

In der Auswertungsebene erfolgt das Eingeben bzw. Einlesen der Daten und deren Darstellung in einem geeigneten Koordinatensystem. Folgende kartesische Koordinatensysteme stehen zur Auswahl: physikalisches, mathematisches und logarithmisches Koordinatensystem mit ihren verschiedenen Varianten sowie außerdem ein Polarkoordinatensystem. Die Daten können mit verschiedenen Symbolen in beliebiger Größe und Farbe oder als Balkengrafik (Treppen, Histogramme etc.) in den Koordinatensystemen dargestellt und mit Fehlerbalken versehen werden. Zusätzlich kann man verschiedene Interpolations- und Approximations-Algorithmen zur Kurvenanpassung verwenden. Die Meßreihen und Graphdaten bleiben im RAM-Speicher und müssen nicht auf Disk ausgelagert werden. Der Benutzer kann über eine komfortable Dialogbox direkt in die Speicherverwaltung der Auswertung eingreifen. Man kann z.B. mit Recall bestimmte Meßreihen und Kurven aus der Auswertung hervorgreifen und als aktuell erklären, um sie im Nachhinein weiter zu verarbeiten oder zu verändern. Es läßt sich sowohl eine komplette Auswertung auf Disk abspeichern als auch separat einzelne Kurven, Meßreihen, Glättungsparameter, Statistikwerte oder Grafiken. Natürlich können die Dateien jeweils getrennt wieder eingeladen werden, um Änderungen vorzunehmen. Eine nachträgliche Manipulation einer Auswertung (z.B. Neukalibrierung der Graphdaten), ist deshalb möglich, weil die REAL-Daten mit abgespeichert werden und die Auswertung nicht nur als Grafik vorliegt. In der Vektor-Grafik-Ebene kann die Auswertung mit zusätzlichen Grafikfunktionen erweitert werden. Die Zusammenstellung mehrerer Auswertungen auf einem Blatt findet auf der dritten Ebene in einem Layout-Window statt. Ähnlich wie in DTP Programmen befinden sich die Auswertungen und Grafiken innerhalb frei verschiebbarer skalierbarer Rahmen.

Veränderungen

Änderungen am Koordinatensystem, z.B. der Tick-Marks, der Marker, der Beschriftung usw., können interaktiv durchgeführt werden. Hier einige Beispiele: Ein Doppelklick mit der Maus in ein Koordinatensystem öffnet eine Dialogbox, in der man eine Diashow der verschiedenen Varianten des Koordinatensystems vorgeführt bekommt. Verschiedene Raster lassen sich, getrennt für x/y-Achse, einblenden. Auch den Hintergrund und die Umrandung des Koordinatensystems kann man ändern. Mit einem Einfachklick läßt sich das Koordinatensystem in freidefinierbarer Größe verändern. Klickt man die Nachkommastellen der Koordinatenskalierung an, öffnet sich an der momentanen Mausposition eine Dialogbox, in der man die Nachkommastellen und das Zahlenformat (normal, scientific 1, scientific 2 und technical) einstellen kann. Ein anderes Beispiel wäre die Veränderung der Überschrift: Mausklick auf die Überschrift, Maus festhalten und an neue Position schieben. Doppelklick auf die Überschrift: Editieren des Textes und Einstellung der Textattribute (z.B. anderer GDOS-Font). Zieht man das Auswerte-Icon in das Bearbeitungsfenster, lassen sich die Intervallgrenzen manuell oder automatisch (Auto-Scale) korrigieren. Bewegt man einen Graph mit der Maus über den Bildschirm, läßt er sich an einer beliebigen Position absetzen. Auf Wunsch werden die Graphdaten anschließend auf die neue Position umgerechnet. Sämtliche interaktiven Funktionen lassen sich auch im Pull-Down-Menü auswählen oder über die Tastatur mittels Shortcuts aufrufen.

Appoximation/Interpolation

Eindeutig liegt eine der Stärken von DATA in der Vielfalt der Regressions-, Approximations-, und Interpolations-Algorithmen [1]. Findet man trotzdem keine geeignete Kurve, stehen zusätzlich zwei Kurvenlineale (B-Spline u. Bezier) zur Verfügung, die man mit Hilfe der Maus frei biegen und ziehen kann; die resultierende Kurve wird anschließend in Weltkoordinaten umgerechnet. Natürlich ist auch ein beliebiger Funktions-Plot möglich. Mit diesem kann man dann auch die Kurven über das Daten-Intervall hinaus extrapolieren. In der DATA-Version 3.1 sind zwei neue Algorithmen hinzugekommen: Das Fitpolynom 0-9ten Grades, welches eine Alternative zum Householder-Fit darstellt, und der Simplex-Algorithmus. Der Simplex-Algorithmus ist ein besonders unter Naturwissenschaftlern bekanntes Verfahren, um beliebige rationale Funktionen an vorgegebene Meßreihen anzupassen. Genau wie beim Gaußschen Fitpolynom wird über den integrierten Formel-Parser (Bild 4) eine Funktionsgleichung explizit eingegeben. Diese kann verschiedene Parameter und Konstanten beinhalten, die DATA auf Wunsch an die Daten angleicht. Parallel zur Berechnung des Fits kann ein Report in einem Window, auf Disk oder auf einem Drucker ausgegeben werden. Dieser dokumentiert den Berechnungsablauf und die Ergebnisparameter. Anschließend wird der Graph der angefitteten Funktion ins Koordinatensystem eingetragen. Da das Berechnungsverfahren des Simplex-Algorithmus’ im Detail sehr interessant ist, verweise ich auf die Original-Veröffentlichung [2]. Die einzelnen Approximations- und Interpolations-Algorithmen sind im DATA-Handbuch ausreichend beschrieben.

Mathematische Spiele

Tatsächlich ist es spielend leicht, in DATA mathematische Berechnungen durchzuführen. Vorweg aber eine nichtmathematische Methode, um Daten-Ausreißer zu fangen: Oft kommt es vor, daß man Meßreihen hat. in denen sich Ausreißer oder fehlende Werte („missing value“) befinden. Die Ausreißer möchte man natürlich getrennt von den brauchbaren Daten bearbeiten, sie lassen sich nur leider funktional schlecht einordnen. Bei 2000 Meßdaten kann das leicht zur Verzweiflung des Anwenders führen, falls der beabsichtigt, die komplette Datenreihe zu editieren. DATA hat für diese Fälle ein sog. Lasso (Anwendung wie bei Malprogrammen) zur Verfügung. Hat man die Ausreißer mit dem Lasso eingefangen, erscheint unmittelbar danach an der aktuellen Mausposition ein Pull-Up-Menü, in dem man verschiedene Funktionen auswählen kann (z.B. Ausreißer löschen, Statistik der Ausreißer usw.). Lustig finde ich die Möglichkeit, die Ausreißer mit der Maus an ihren eigentlichen Platz schieben zu können. Wichtige mathematische Anwendungen auf Meßreihen sind: Kalibrierung, Substitution und Transformation der Meßdaten. Dazu findet man getrennte Dialogboxen in DATA. Der Hauptschwerpunkt der Datenmanipulation geht von einem mit Buffer-Funktion betitelten Taschenrechner-Icon aus. Klickt man das Icon an, erscheint eine umfangreiche Dialogbox, in der man bis zu 24 interne Speicher zur Zwischenspeicherung der aktuellen Daten-Arrays (Meßdaten, Graphdaten. Fehlerdaten und Glättungsparameter) benutzen kann. Speicherund Daten-Arrays können beliebig vertauscht werden. So ist es z.B. möglich, die y-Werte einer Meßreihe von denen einer zweiten zu subtrahieren und als neue Meßreihe darzustellen und die neuen Daten durch eine Kurve zu interpolieren. Ebenfalls in dieser Dialogbox befindet sich ein Button zur Aktivierung einer mathematischen Funktion, die über ein integriertes Pull-Up-Menü ausgewählt werden kann. Findet man darin nicht die passende Funktion, kann man über den Formel-Parser eine eigene Funklionsgleichung definieren und diese anschließend auf die Daten- und Speicher-Arrays anwenden. Ferner kann man eine Statistik der Arrays ausgeben. Edit ruft den DATA-Daten-Editor auf. Die Speicher-Arrays können als Matrix im ASCH-Format (max. 10000 Zeilen/max. 24 Spalten) abgespeichert und wieder eingelesen werden. Im Handbuch ist der Source-Code der Laderoutine angegeben. Für die Integration von Kurven steht ein eigenes Menü-Window zur Verfügung. Zur Integralbildung einer Kurve kann man verschiedene Nullpunktskorrekturen vornehmen, das Muster und den Beschriftungstext auswählen und einen Report ausgeben lassen. Zur Nullpunktskorrektur stehen zur Verfügung: horizontaler Offset, lineare Kurve und Kurvenlineal (jeweils mit der Maus definierbar). Zusätzlich kann man auch hier über den Formel-Parser eine beliebige Funktionsgleichung angeben, die dann als Nullpunktskorrektur verwendet wird. Damit man die Funktionen nicht immer wieder neu eingeben muß, lassen sie sich mit den Parametern auf Disk abspeichern.

Das Blatt vor Augen

Neu in der Version 3.1 ist die beliebige Größe eines Blattes (voreingestellte Formate. z.B. DIN A3 oder frei wählbare Maße). Es kann immer nur ein Blatt bearbeitet werden. Durch die Fenstertechnik kann man in jeden Bereich scrollen. Auch die komplette Seite läßt sich auf dem Bildschirm darstellen (Preview). Auch nach dem Umschalten zum Preview-Modus kann man interaktiv Weiterarbeiten; alle Funktionen sind zugänglich. Wichtig ist, daß alle Diagramme und Objekte millimetergenau plaziert werden können. Das erleichtert das Layout wesentlich.

Beschriftung

Neben den obligatorischen Achsenbeschriftungen und Überschriften können Parametertexte und Legenden dargestellt werden. Auch Indizes (Superscript/Subscript) sind möglich. Die Beschriftungen sind sowohl manuell als auch automatisch positionierbar. Bei Größen- oder Positionsänderungen des Koordinatensystems bewegen sich die Beschriftungen bei automatischer Positionierung mit. Auch im Vektor-Grafik-Editor ist eine Textfunktion integriert, die zusätzliche Beschriftungsmöglichkeiten bietet. Bei Serien-Auswertungen kann die Beschriftung als Schablone beibehalten werden. DATA verwendet zur Beschriftung proportionale GDOS-Fonts. Damit kann man auf ein vielfältiges Schriftenangebot zurückgreifen. Auch Signum2-Fonts sind dank des Programms Tschidos (Maxon-Sonderdisk 57) konvertiert verwendbar. DATA unterstützt auch ID.-Nr. jenseits 256. Die Fontgröße hängt nur vom Zeichensatz ab und wird in Millimeter angegeben. Die Fonts müssen genauso wie die Device-Treiber im Assign.Sys-File angemeldet sein.

Zeichnen mit Vektorgrafik

Ab DATA 3.0 ist das Pixel-Malprogramm früherer DATA-Versionen durch ein vektoriell arbeitendes Zeichenprogramm ersetzt worden. Da der übrige Teil des Programms bereits seit der Version 2.0 objektorientiert arbeitete, war es längst an der Zeit, den Grafikteil umzustellen. Erwähnen möchte ich an dieser Stelle nur, daß die Umsetzung von Pixelgrafik auf Vektorgrafik gut gelungen ist und daß die Vektorgrafik in einem eigenen Window bearbeitet wird (Bild 6). Positionsverschiebungen und Größenänderungen der Grafik sind jedoch auch innerhalb des Auswerte-Windows möglich. Über ein spezielles Icon läßt sich auch im Grafik-Window das Koordinatensystem einblenden. Kennt man das Zeichenprogramm Arabesque, kommt man auf Anhieb mit dem Vektorteil zurecht.

Dateioperationen

DATA verwaltet insgesamt fast 20 verschiedene Dateiformate (inkl. acht Grafikformate), von denen die meisten auch wieder eingelesen werden können. Vorteilhaft ist, daß der interne Pfad- und Dateimerker sich alle Ordner und File-Namen merkt. Zusätzlich liest DATA verschiedene ASCII-Datenformate ein, damit man auch Fremdformate einiesen kann. Das bekannteste Grafik-Dateiformat ist das GEM-Metafile für Vektor-Grafik und das GEM-Image-Format für Pixelgrafik. Die Pixelformate (Image, STAD, Screen, Degas, GFA und Degas) und das Metafile können nur geschrieben werden. Das eigene Vektorformat ('*.VEK’) kann sowohl geschrieben als auch eingelesen werden. Insgesamt lassen sich abspeichern/einlesen: Layout, Auswertung, Meßdaten, Graphdaten, Glättungsparameter, Grundeinstellungen, Systemkonfigurationen, Makros, Vektor-Grafik, Funktionen und Parameter, Statistikwerte, Reports und die Buffer-Matrix.

Makros

Treten bei Serien-Auswertungen wieder kehrende Arbeitsabläufe auf, kann man DATA dazu überreden, diese in Form von Makros auswendig zu lernen. Man führt DATA den Vorgang einmalig vor, gibt dem ganzen einen Namen, legt das Makro z.B. auf die Funktionstaste F2 und drückt in Zukunft bei jeder neuen Datenmenge nur noch die Taste F2.

Zusätzlich zu den Menüaufrufen können auch die wichtigsten Dialogboxen automatisch bedient werden. Z.B. kann eine Formel über ein Makro in den Formel-Parser eingetippt werden, oder in der Buffer-Dialogbox können automatisch Daten-Arrays manipuliert werden.

Das Handbuch

Das Programm wird mit einem ca. 300seitigen eingebundenen Buch im DIN-A4-Format und einem Beispielhandbuch in Form einer Arbeitsmappe ausgeliefert. Das Handbuch hat mir persönlich sehr gut gefallen, da es sowohl die einzelnen Menüpunkte detailliert beschreibt, als auch die mathematischen Funktionen und Algorithmen. Zur guten Übersicht trägt besonders das ausführliche Index- und Inhalts-Verzeichnis bei. Arbeitet man anhand des Beispielhandbuchs die in bebilderter Form dargestellten Übungsbeispiele durch, bekommt man einen schnellen Überblick über die Möglichkeiten, die das Programm einem bietet.

Fazit

Das Programm DATA 3.1 ist sowohl für den professionellen Einsatz bei der Auswertung und Präsentation größerer Datenmengen als auch für den gelegentlichen Gebrauch. z.B. im Studium für die Auswertung von Praktikumsversuchen oder die Diplomarbeit, sehr zu empfehlen. Das Programm besticht sowohl durch seinen großen Bedienungskomfort als auch durch die hohe Arbeitsgeschwindigkeit. Große Schwachpunkte habe ich nicht gefunden. Trotzdem würden ein Tabellengenerator, 3D-Grafik und vielleicht auch Tortengrafik das Programm abrunden. Die Preise von DM 398,- für die Professional-Version und von DM 198,- für die normale Version liegen deutlich unter den Erwartungen. Bei der normalen Version ist die Anzahl der Meßpunkte/Stützstellcn pro Meßreihe auf 128 begrenzt. Bei der Professional-Version ist die Anzahl nur vom RAM-Speicher abhängig. Ich glaube zum Abschluß sagen zu dürfen, daß DATA inzwischen zu einem Maßstab geworden ist, an dem sich Programme dieser Art orientieren müssen.

K. P. Dickscheidt

Bezugsquelle:

Dipl.-Phys.-Ing. Ralf Wirtz Kasterstraße 30 W 5170 Jülich

Literatur

[1] Ein Meßwert kommt selten allein - Grafische Analyse mit Data, ST-Computer 4/89, S. 26-31

[2] Fitting Curves to Data - The simpler algorithm is the answer, M S. Caceri and W.P. Cacheris, Florida State University, BYTE Max 1984

---

---