Oft findet man in Computerzeitschriften und -büchern Programme in allen möglichen Sprachen, die Berechnungen oder graphische Darstellungen mit mathematischen Funktionen durchführen. Meist sind jedoch die Formeln fest im Programm „eingebaut“, und Änderungen können zum Teil mit erheblichem Aufwand verbunden sein, insbesondere wenn man mit Compilern arbeitet.
Wer mit einem BASIC-Interpreter herkömmlicher Art arbeitet, der über die Befehle CHAIN und MERGE verfügt, kann sich mit einem Trick aus der Patsche helfen. Wie in Listing 1 gezeigt ist es möglich, über den Umweg einer Diskettendatei ein sich selbst veränderndes Programm zu schreiben.
Programmiert man jedoch in einer Compilersprache oder z. B. mit dem enorm leistungsfähigen GfA-BASIC-Interpreter, kommt man mit solchen Kniffen nicht mehr weiter.
Hier hilft alles nichts, man muß sich sozusagen zu Fuß durch eine als Zeichenkette eingegebene Formel „beißen“ und Zeichen für Zeichen analysieren.
So aufwendig, wie das auf den ersten Blick scheinen mag, ist dies nun auch wieder nicht; das Zauberwort, das hier weiterhilft heißt Rekursion.
Schauen wir uns doch einmal eine Formel - einen arithmetischen Ausdruck wie die Mathematiker sagen - genauer an. Zur graphischen Verdeutlichung sollen hier sogenannte Syntax-Diagramme, ähnlich wie man sie zur Definition von PASCAL-Befehlen verwendet, weiterhelfen. Bild 1 erklärt die möglichen Symbole. Syntax-Diagramme werden in Pfeilrichtung auf Flußlinien durchlaufen; diese können sich an verschiedenen Stellen aufspalten und so Möglichkeiten zur Verzweigung und Schleifenbildung beschreiben. Die Kästchen mit den abgerundeten Ecken dienen nur der Namensgebung des jeweiligen Diagramms und können einfach übergangen werden.
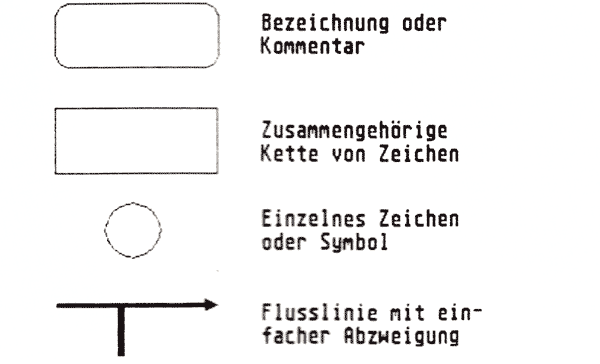 Bild 1: Definition der für die Syntax-Diagramme verwendeten Symbole
Bild 1: Definition der für die Syntax-Diagramme verwendeten Symbole
Unsere Formel kann nun als Kette von Zeichen, die sich in bestimmte Teilketten zerlegen läßt, mit diesem Schema formal beschrieben werden.
So, wie man den arithmetischen Ausdruck von links nach rechts zu Papier bringt, kann man den Flußlinien folgen und, gemäß der mathematischen Hierarchie der Rechenregeln, von einer Grobdarstellung zu immer weiteren Unterteilungen gelangen.
Wohlgemerkt, Syntax-Diagramme sind weder Flußdiagramme noch dienen sie zur exakten Darstellung eines Programmablaufs, jedoch lassen sich die durch sie beschriebenen Regeln leicht in entsprechende Programm-Algorithmen umsetzen.
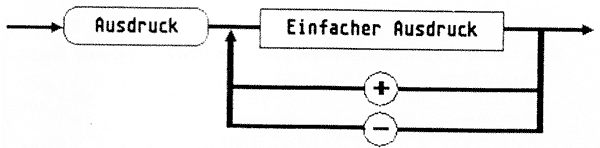 Bild 2
Bild 2
In Bild 2 ist nun allgemein ein arithmetischer Ausdruck dargestellt, der aus beliebig vielen einfachen Ausdrücken besteht, die über das Plus- oder Minuszeichen verknüpft sein können. Dies ist durch die Abzweigung hinter dem Käsen „Einfacher Ausdruck“ verdeutlicht, was bedeutet, daß hier abgebogen wird solange einem Teilausdruck ein Plus- oder Minusoperator folgt.
Beispiel:
6.89 + (3/7.8-5)*5 - sin(exp(-3*7/8)) + ...
6.89, (3/7.8 - 5)5, sin(exp(-37/8)) sind Teilausdrücke des o. g. arithmetischen Audrucks
Jeder einfache Ausdruck setzt sich aus einzelnen Termen zusammen, die über Multiplikation oder Division verknüpft sind (Bild 3).
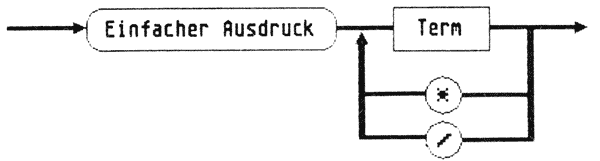 Bild 3
Bild 3
Ein Term ist ein vorzeichenbehafteter Faktor, der gegebenenfalls wiederum mit einem vorzeichenbehafteten Faktor potenziert sein kann (Bild 4).
 Bild 4
Bild 4
Ein vorzeichenbehafteter Faktor besteht aus einem vorzeichenlosen (positiven) Faktor mit eventuell vorangestelltem negativem Vorzeichen (Bild 5).
Wie in Bild 6 zu sehen, ist nun ein Faktor entweder eine positive reelle Zahl (die sich aus Ziffern, eventuell Dezimalpunkt und/oder Exponent zusammensetzt), ein in Klammern stehender arithmetischer Ausdruck, eine Variable (hier als „x“ bezeichnet) oder eine mathematische Funktion, deren Argument selbst wieder ein Faktor ist.
Listing 2 zeigt ein GfA-BASIC Programm, welches das Modul FORMEL. MRG enthält. Hier wird gezeigt, wie sich konsequent oben genannte Regeln ine ine Hochsprache umsetzen lassen. GfA-BASIC ist hierzu ebenso geeignet wie PASCAL oder C. Eine Umsetzung des Moduls in eine dieser Sprachen sollte daher keine Probleme bereiten. Bei FORMEL.MRG handelt es sich um ein universell benutzbares Teilprogramm, das leicht an unterschiedliche Anwendungen angepaßt werden kann.
Das eigentliche Hauptprogramm mit der Procedure Def_funktion dient nur der Demonstration von FORMEL.MRG. Das hier vorgestellte Modul kann sehr vielseitig verwendet werden, z. B. für einen selbstprogrammierten Taschenrechner, ein Funktionsplotprogramm oder die Analyse von mathematischen Funktionen. Erweiterungen mit beliebig komplexen Funktionen sind leicht durchzuführen, wie im Programmtext an entsprechender Stelle kommentiert wurde.
Ich hoffe, FORMEL.MRG gibt viele Anregungen für eigene Ideen und wünsche viel Spaß beim Programmieren.
(H. Bauch)
 Bild 5
Bild 5
'****************************************************
'* *
'* --- ST_FORM.BAS --- *
'* Beispiel zur Berechnung beliebiger Formeln *
'* mit dem ST-BASIC-Interpreter *
'* *
'* (c) 22.11.1986 H. Bauch *
'* *
'****************************************************
Clearw 2:Fullw 2
Print
Print " F O R M E L B E R E C H N U N G "
Print " ---------------------------------"
Print
gosub Funktion.def
'
Anfang:
Input " x = ",xS
If x$<>"N" and x$<>"n" Then
Print " f(x) = ";fny(val(x$)),"<N> für neue Funktion !"
Else Gosub Funktion.def
Goto Anfang
'
'
Funktion.def:
Print
Print " Definition einer beliebigen Funktion in BASIC-Syntax"
Print
Input " f(x) = ",Formel$
Open "O",#1,"FKT.BAS"
Print#1,"200 Def fny(x) = "+Formel$
Close #1
Chain Merge "FKT.BAS",200
' Die nächste Zeile wird vom Programm verändert:
Def fny(x) = 1/(sqr(1-x^2))
Return
' ***********************************************************
' * *
' * -- FORMULA.BAS -- *
' * Ein Testprogramm für das Modul FORMEL.MRG *
' * *
' * (c) 23.11.1936 H. Bauch *
' * Taunusstr. 96 *
' * 6237 Liederbach *
' * *
' ***********************************************************
'
' --- Konscantendefinitionen
'
True:=-1
False!=0
'
'
' ----------------------------------------------------------------
' ---------- Beginn des Hauptprogramms zum -----------------------
' ---------- Testen des Moduls FORMEL.MRG: -----------------------
' ----------------------------------------------------------------
'
Cls
Print
Print
Print " F O R M E L B E R E C H N U N G "
Print " ---------------------------------"
Print
Print " (c) 1986 H. Bauch"
Print
First!=True!$
@Def_funktion
'
Do
Input " x = ",X$
If Val?(X$)<>0 X=Val(X$)
@Berechnung(Formel$,X)
Print " f(x) = ";Berechnung,
Print "Für neue Funkion <N> eingeben !"
Print
Else
If Upper$(X$)="N"
@Def_funktion
Endif
Endif
Loop
'
' -------------------------------------------------------
' ------------- Ende des Hauptprogramms -----------------
' -------------------------------------------------------
'
'
Procedure Def_funktion
'
' ----------------------------------------------------------------
' Dieses Unterprogramm dient nur zu Testzwecken; es ermöglicht
' erstmaliges und wiederholtes Definieren einer Formel/Funktion in
' Form eines Strings. Funktionen können auch konstant sein, d. h.
' es kommt keine Variable (hier "x") in ihr vor.
' ----------------------------------------------------------------
'
' Globale Variable: True!,False!,First!,F_max%,Std_funktion$(),
' Formel$, Fehler_positon%
Local I%,Xtest,Fehleraus$
'
If First!
@Init_berechnung
First!=False!
Print
Print " Definition einer beliebiger. Funktion in BASIC-Syntax"
Print
Print " Standardfunktionen: "
Print
Print " / ";
For I%=1 To F_max%
Print Std_funktion$(1%);" / ";
Next I%
Endif
Print
Print
Repeat
Input " f(x) = ",Formel$
' -----------------------------------------------------------------
' An dieser Stelle wird die @Berechnung() zunächst mit einem Test-
' wert aufgerufen; in einigen Fällen kann es bei dem hier gewählten
' Wert zum Fehlerabbruch kommen, weil sich z. B- Division durch
' Null oder Wurzel aus negativer Zahl ergibt.
' Ein einfacher Syntaxfehler wird so jedoch aufgedeckt.
' -----------------------------------------------------------------
Xtest=0.0123
@Berechnung(Formel$,Xtest)
If (Fehler_position%<>0)
Fehleraus$="Fehler in der Formel!an Position "+Str$(Fehler_position%)
Alert 1,Fehleraus$,1," Weiter ", Dummy
Endif
Until (Fehler_position%=0)
Return
'
'
' ***********************************************************
' * *
' * --- FORMEL.MRG--- *
' * Berechnung einer beliebigen Funktion als String *
' * *
' ***********************************************************
'
Procedure Init_berechnung
'
' ------------------------------------------------------------------
' Dieses Unterprogramm dient zur Initialisierung der benutzbaren
' Standardfunktionen für die Procedure Faktor; Erweiterungen können
' dort leicht eingefügt werden, Funktionsnamen müssen in der DATA-
' Zeile ergänzt werden und F_max% muß angepaßt werden.
' Init_berechnung muß stets vor der Procedure Berechnung aufgerufen
' werden.
' ------------------------------------------------------------------
'
' Globale Variable: F_max%,
' Std_funktion$()
Local I%
'
' Anzahl z.Zt. implementierter Standardfunktionen:
F_max%=9
'
' Standardfunktionen festlegen
Dim Std_funktion$(F_max%)
Data ABS,SQR,SIN,COS,TAN,ATN,LN,LOG,EXP
Restore
For I%=1 To F_max%
Read Std_funktion$(I%)
Next I%
Return
'
'
Procedure Berechnung(Funktion$,X)
'
' ------------------------------------------------------------------
' Dies ist die Hauptroutine des Moduls FORMEL.MRG; nach Aufruf von
' von Init_berechnung wird stets hier eingesprungen. In einem Haupt-
' programm können verschiedene Formeln benötigt werden; diese werden
' einfach jeweils neu durch den Stringparameter Funktion$ übergeben.
' Z. Zt. ist nur eine Variable (X) in der Procedure Faktor vorge-
' sehen, Erweiterungen auf beliebig viele Variable sind möglich
' durch Ergänzung der Parameterliste und Erweiterung der Procedure
' Faktor an der dort bezeichneten Stelle.
'
' Sollte in Funktion$ ein Syntax-Fehler gefunden werden, so wird
' Fehler position% als Global zurückgegeben. '
'
' Da GfA-BASIC keine Function im Sinne von PASCAL besitzt, werden die
' Ergebnisse einer Procedure als Variable mit dem Namen der Proce-
' dure zurückgegeben.
' ------------------------------------------------------------------
'
' Globale Variable: True!, False!, F_max%, Berechnung, Fehler_position%
' Std_funktion$(), Berechnung
'
Local Zeil_ende$,Position,Zei$,Ausdruck
'
Zeil_ende$=Chr$(0)
Position%=0
@N_zeichen
@Ausdruck
Berechnung=Ausdruck
If Zei$=Zeil_ende$
Fehler_position%=0
Else
Fehler_position%=Position%
Endif
Return
'
'
Procedure Ausdruck
'
Local E,Einf_ausdruck,Operator$
'
@Einf_ausdruck
E=Einf_ausdruck
While Zei$="+" Or Zei$="-"
Operator$=Zei$
@N_zeichen
If Operator$="+"
@Einf_ausdruck
E=E+Einf_ausdruck
Endif
If Operator$="-"
@Einf_ausdruck
E=E-Einf_ausdruck
Endif
Wend
Ausdruck=E
Return
'
'
Procedure Einf_ausdruck
'
Local S,Term,Operator$
'
@Term
S=Term
While Zei$="*" Or Zei$="/"
Operator$=Zei$
@N_zeichen
If Operator$="*"
@Term
S=S*Term
Endif
If Operator$="/"
@Term
S=S/Term
Endif
Wend
Einf_ausdruck=S
Return
'
'
Procedure Term
'
Local T,Vorz_faktor
@Vorz_faktor
T=Vorz_faktor
While Zei$="*"
@N_zeichen
@Vorz_faktor
T=T^Vorz_faktor
Wend
Term=T
Return
'
'
Procedure Vorz_faktor
'
Local Faktor
'
If Zei$="-"
@N_zeichen
@Faktor
Vorz_faktor=-Faktor
Else
@Faktor
Vorz_faktor=Faktor
Endif
Return
'
'
Procedure Faktor
'
Local F,I%,L%,Beginn%
'
If Zei$>="0" And Zei$<="9"
' --------------------------------------------------------
' "Zusammenbasteln" einer Zahlen-Konstante
' --------------------------------------------------------
Beginn%=Position%
Repeat
@N_zeichen
Until Not (Zei$>-"0" And Zei$<="9")
If Zei$="."
Repeat
@N_zeichen
Until Not (Zei$>="0" And Zei$<="9")
Endif
If Upper$(Zei$)="E"
@N_zeichen
Repeat
@N_zeichen
Until Not (Zei$>="0" And Zei$<="9")
Endif
F=Val(Mid$(Funktion$,Beginn%,Position%-Beginn%))
Else
If Zei$="("
' ----------------------------------------------------
' Faktor ist ein geklammerter Ausdruck, d.h.
' rekursiver Aufruf der Procedure Ausdruck
' ----------------------------------------------------
@N_zeichen
@Ausdruck
F=Ausdruck
If Zei$=")"
@N_zeichen
Else
Fehler_position%=Position%
Endif
Else
If Upper$(Zei$)="X"
' -----------------------------------------------------
' Variable der Formel gefunden!
' Hier können Erweiterungen für beliebig viele Variable
' "eingebaut" werden; siehe auch Kommentar zu Beginn der
' Hauptroutine Procedure Berechnung().
' -----------------------------------------------------
@N_zeichen
F=X
Else
' -----------------------------------------------------------
' Suche nach Standardfunktions-Namen wie bei
' Procedure Init_Berechnung in der Data-Zeile vereinbart!
' Hier können noch beliebig viele Funktionen ergänzt werden
' (z.B. arcsin, arccos, Fakultit, hyperbol. Funktion usw.).
' -----------------------------------------------------------
Erfolg!=False!
For I%=1 To F_max%
If Erfolg!=False!
L%=Len(Std_funktion$(1%))
If Upper$(Mid$(Funktion$,Position%,L%))=Std_funktion$(1%)
Position%=Position%+L%-1
@N_zeichen
@Faktor
F=Faktor
If I%=1
F=Abs(F)
Endif
If I%=2
F=Sqr(F)
Endif
If I%=3
F=Sin(F)
Endif
If I%=4
F=Cos(F)
Endif
If I%=5
F=Tan(F)
Endif
If I%=6
F=Atn(F)
Endif
If I%=7
F=Log(F)
Endif
If I%=8
F=Log10(F)
Endif
If I%=9
F=Exp(F)
Endif
Erfolg!=True!
Endif
Endif
Next I%
If Not Erfolg!
Fehler_position%*=Position%
Endif
Endif
Endif
'
Endif
Faktor=F
Return
'
'
Procedure N_zeichen
'
Repeat
Inc Position%
If Position%<=Len(Funktion$)
Zei$=Mid$(Funktion$,Position%,1)
Else
Zei$=Zeil_ende$
Endif
Until Zei$<>" "
Return
'
'
' -----------------------------------------------------------
' ------------- Ende des Moduls FORMEL.MRG ------------------
' -----------------------------------------------------------
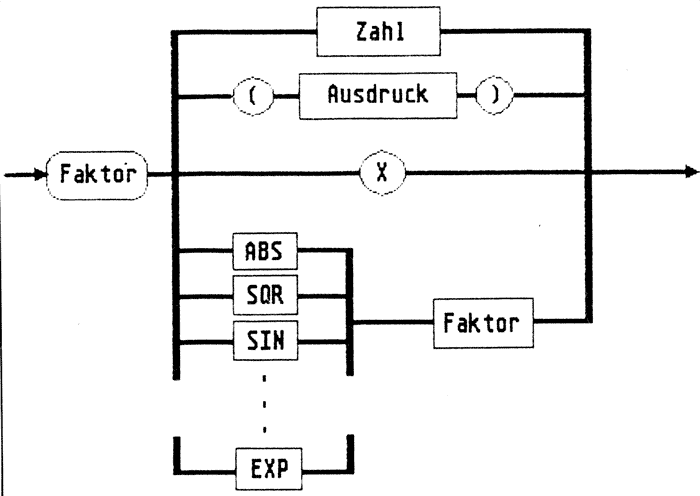 Bild 6
Bild 6