
Der Autor
Dr. Karl Sarnow
wird Sie mit dieser Serie in die Welt der künstlichen Intelligenz einführen.
Er studierte Physik an der TU Hannover und unterrichtet zur Zeit an einem Gymnasium die Fächer Mathematik, Physik und Informatik.
Anfang 1986 stieg er auf den ST um und kommuniziert mit ihm in allen nur erdenklichen Sprachen. Seine bevorzugten Programmiersprachen sind C, LISP und Prolog.
Zum Geleit
Dieser Artikel ist der erste in einer Reihe von Aufsätzen, in denen ich Ihnen Probleme und Verfahrensweisen, die im Bereich der künstlichen Intelligenz vorliegen, nahebringen möchte. Dabei werde ich mich bemühen, die beiden aktuellen Sprachen der KI — LISP und PROLOG - in gleicher Weise zu berücksichtigen. Da beide Sprachen im Public-Domain-Service der ST-Computer-Redaktion vorliegen, sollte es dem Leser nicht schwerfallen, diesem Kurs zu folgen. Übrigens hat jeder ST-Besitzer ja schon von Haus aus die ausgezeichnete Version einer Kl-Sprache mitbekommen: Die (viel zu wenig beachtete Logo-Version von Digital Research, die ich bei dieser Gelegenheit gerne aufwerten möchte. LOGO ist nicht nur die Turtle-Sprache für Kinder. Als LISP-Derivat ist LOGO ohne Schwierigkeiten in der Lage, das zu vollbringen, was LISP kann. Deshalb werde ich die entsprechende LOGO-Variante ebenfalls erläutern. Jeder Kurs ist einem Schwerpunkt gewidmet und behandelt die für das entsprechende Thema geeigneten Funktionen (LISP, LOGO) bzw. Prädikate (PROLOG). Für eine Übersicht über LISP und PROLOG und die allgemeinen Anwendungsgebiete der KI sei auf meine bisher in dieser Zeitschrift erschienenen Artikel verwiesen (Heft Nr. 1/86 und 3/86). Natürlich wird es sich nicht vermeiden lassen, daß das eine oder andere Thema vorrangig in einer der drei Sprachen behandelt wird und die anderen Sprachen etwas zurücktreten. Ich möchte jedoch den Überblick über die Methoden der KI von der Einengung der jeweils verwendeten Sprache befreien und andererseits die spezifischen Eigenschaften der jeweiligen Sprache erhalten.
Atome und Listen als Datenelemente
Bei Problemen der künstlichen Intelligenz tritt die Rechenfertigkeit hinter der Fähigkeit der Symbolmanipulation zurück. Logischerweise bedient man sich hierzu anderer Datenstrukturen als für die Bearbeitung arithmetischer Probleme. Die beiden Datentypen, mit denen wir uns hauptsächlich beschäftigen, sind Atome und Listen (einzige Ausnahme: Objekte in XLISP, siehe Literaturliste 2. Atome (gr.: atomos, unteilbar) sind Datenelemente, die nicht weiter strukturiert sind und folglich auch nicht in kleinere Bestandteile zerlegt werden können. Dies können symbolische Namen sein (hallo, auto, champagner, hexamethylentetramin, ...) oder Zahlen. Im letzten Fall spricht man von numerischen Atomen.
Listen sind im einfachsten Fall nicht anders als miteinander verbundene Atome. In LISP werden die einzelnen Elemente einer Liste von runden Klammern eingeschlossen, in PROLOG und LOGO von eckigen. Also ist
(hallo auto 3.141)
bzw.
[hallo, auto, 3.141]
eine Liste in LISP, LOGO bzw. PROLOG, welche die Atome hallo, auto und 3.141 enthält. Allerdings können Listen wiederum Listen als Elemente enthalten [(Rekursion, ick hör dir trapsen!)]. Ein etwas sinnvolleres Beispiel wäre (LISP-Notation):
(rufname (vornamel vorname2 vorname3) name)
Auf die natürliche Intelligenz des Lesers vertrauend, verzichte ich auf die PROLOG- und LOGO-Schreibweise.
In dieser Liste werden die Patennamen als Unterliste geführt. Die Liste selbst besteht also aus drei Elementen, den Atomen rufname und name sowie der Liste mit den drei Patennamen. LISP schießt in Sachen Listenbehandlung den Vogel ab, weil der Interpreter jeden Befehl in Listenform erwartet.
Die einfachsten Beispiele für Listenverarbeitung stammen deshalb in LISP aus dem Bereich der Arithmetik - ein Indiz für den Wahrheitsgehalt der Vermutung, daß reine Rechenfähigkeit und Intelligenz wenig korreliert sind.
Gibt man in LISP die folgende Liste ein, interpretiert sie der Interpreter als einen auszuführenden Befehl und gibt prompt das Ergebnis der Ausführung bekannt (fett: Benutzereingabe, kursiv: Antwort des Interpreters).
(+ 1 2)
3
Da XLISP ein eval_LISP ist (siehe Literaturliste 2), erkennt das System beim Versuch, die Liste zu evaluieren, daß das erste Element der Liste ein Atom ist, das die Bedeutung einer im System eingebauten Funktion hat, und führt die Funktionsberechnung durch. Solche im System eingebauten Funktionen tragen die Bezeichnung Primitiv. Am Beispiel der Addition in LISP kann man auch einen Vorteil der Liste gegenüber anderen Datenstrukturen erkennen. So erlaubt LISP mehr als 2 Argumente bei allen arithmetischen Operationen:
(+ 1 2 3 4 5)
15
(★ 2 4 3)
24
Listen in den Kl-Sprachen haben zudem den Vorteil, daß ihre Elemente typenlos sind (im Gegensatz zu PASCAL oder C). Beispielsweise werden die folgenden beiden Listen gleichwertig als Einträge einer Gehaltsliste akzeptiert:
(schmidt emil 1200.50)
(meier (hans georg gustav) 3179.20)
In allen drei Sprachen werden übrigens die Rechenoperationen in Präfix-Notation angegeben. Nur LOGO als „Anfängersprache“ hat hier dem traditionellen Infix-Denken Tribut gezollt und erlaubt zusätzlich noch die Infix-Notation für arithmetische Operationen. Die Präfix-Notation hat den Vorteil, daß der Operator immer an der gleichen Stelle steht, unabhängig von der Anzahl der Argumente der Operation. Das Umdenken ist zwar lästig, doch wenn die natürliche Intelligenz beim Umgang mit der künstlichen Intelligenz etwas abbekommt, so ist das ein nicht nur erwünschter, sondern beabsichtigter Nebeneffekt.
Zugriff auf Listenelemente
Der Zugriff auf die Listenelemente ist natürlich das A und O der Programmierung in unseren drei Lieblingssprachen. Tab. 1 faßt die elementaren Zugriffsmöglichkeiten in diesen Sprachen zusammen. Verständlicherweise ergibt sich in PROLOG die deutlichste Abweichung von LISP, weil der Zugriff auf die Fakten der Datenbank nur über den Unifizierungsmechanismus (siehe Literaturliste 3) erfolgen kann. Die Prädikate nth/3 und cons/1 in Tab. lc sind benutzerdefiniert und sollten dem jeweiligen Verwendungszweck angepaßt werden.
Die Assoziationsliste
Eine besondere Form von Liste ist in LISP die sogenannte Assoziationsliste (LOGO: Property Liste). Sie ermöglicht das Speichern von miteinander verbundenen Elementen. Weiter unten benutzen wir eine Assoziationsliste, um einen deutschsprachigen Simpeltext in ein holpriges Englisch zu übersetzen. Man speichert dann lediglich in einer Assoziationsliste die deutsch-englischen Assoziationen ab, also im unten aufgeführten Beispiel:
((dies this) (satz sentence) (ist is) (ein a))
Das erste Element einer Assoziationssubliste wird Schlüssel genannt (also: dies, satz, ist, ein). Verschiedene Listenfunktionen in LISP erlauben ein sehr effektives Arbeiten speziell mit dieser Listenform.
| Funktion |
Ausführung in LISP |
| Bindung der Liste (a, b, c) an das Symbol liste |
(setq liste ’(a, b, c)) oder (setq liste (list ’a ’b ’c)) |
Ausgabe des 1. Elementes
a |
(car liste) |
| Ausgabe der Restliste (b, c) |
(cdr liste) |
Ausgabe des 2. Elementes
b |
(car (cdr liste)) oder (cadr liste) |
| Ausgabe des n. Elementes |
(nth n liste) |
| Einfügen eines neuen Elementes x in die Liste. Die neue Liste ist (x, a, b, c) |
(cons x liste) |
| Aneinanderhängen zweier Listen. Ergibt (a, b, c, d, e, f) |
(append ’(a, b, c) ’(d e, f)) |
Tabelle 1a: Elementare Listenoperationen in LISP
Bäume als spezielle Listen
Wir haben schon gesehen, daß die Elemente von Listen wiederum Listen sein können. Diese Datenstruktur nennt man besser einen Baum. Zur Veranschaulichung soll uns die folgende Liste dienen:
(k1 (k2 b1 b2) (k3 (k4 b3 b4) (k5 b5
(k6 b6 b7))))
Den zugehörigen Baum zeigt Abb. 1. Es bedeuten hierin k1 - k6 die Knoten des Baumes, b1 - b7 die Blätter des Baumes. Kenner werden einen sogenannten Binärbaum wiedererkennen; solche, die es werden wollen, lesen bei Literaturliste 4 nach, k1 ist hier die Wurzel des binären Beispielbaumes.
Funktionen in LISP und LOGO
Wir verlassen nun erst einmal den gemeinsamen Teil und kümmern uns speziell um die Organisation eines LISP-bzw. LOGO-Programmes. PROLOG ist eine relationale Sprache, in der das Programm aus Fakten und miteinander verknüpften Klauseln besteht, während LISP und LOGO als funktionale Sprachen ihr Ergebnis aus dem sequentiellen Aufruf von Funktionen erhalten. Wie in Pascal gibt es auch LISP- und LOGO-Programmteile, die zwar behandelt werden wie Funktionen, aber keinen Funktionswert liefern. Sie heißen (wie in Pascal auch) Prozeduren. Allgemein gilt, daß Prozeduren dann keine Funktionen sind, wenn sie Nebeneffekte zeigen. Selbstverständlich gibt es auch in LISP und LOGO standardmäßig vorgesehene Funktionen und Prozeduren; sie heißen Primitive, setq ist ein Beispiel für eine LISP-Prozedur, die keine Funktion ist, weil sie als Nebeneffekt einen Wert (2. Argument) an ein Symbol (1. Argument) bindet. Die Primitive car und cdr in Tab. la sind natürlich Funktionen, die ein entsprechendes Atom bzw. eine Liste als Funktionswert zurückgeben. Und da sie ihr Argument nicht verändern, haben sie auch keine Nebeneffekte. Tab. 2 zeigt eine Zusammenfassung aller Listenprimitive in XLISP mit Beispielen. Um Übersichtlichkeit zu wahren, werde ich hier lediglich die LlSP-Schreibweise erwähnen. Anhand der Tab. 1 sollte der Leser in der Lage sein, die entsprechende LOGO-Schreibweise zu erarbeiten. Die schon in Tab. 1 erwähnten Primitive car, cdr und cons bilden so etwas wie ein Funktions-Umkehrfunktionspaar. D. h., es gilt die Identität:
(cons (car liste) (cdr liste)) = liste
Mit cons wird also eine durch car und cdr aufgetrennte Liste wieder zusammengefügt. Bitte erinnern Sie sich, daß in einer Liste nicht nur Atome, sondern auch Listen als Elemente stehen können. So ist z. B. ((a b) (c d)) eine Liste, die aus zwei Elementen besteht: der Liste (a b) und der Liste (c d). Folglich ergibt (car '((a b) (c d))) den Funktionswert (a b), eine Liste als erstes Element, (cdr '((a b) (c d))) liefert dann logischerweise ((c d)), die Restliste, die die Liste (c d) als einziges Element enthält. Für die in Tabelle 2 aufgeführten Funktionen gibt es noch Optionen, deren Besprechung den Rahmen dieser Einführung sprengen würde. Der Leser sei hier auf das XLISP-Manual verwiesen.
| Funktion |
Ausführung in LOGO |
| Bindung der Liste [A, B, C] an das Symbol LISTE |
MAKE "LISTE [A, B, C] |
| Ausgabe des 1. Elementes A, |
FIRST :LISTE |
| Ausgabe der Restliste [B, C] |
BUTFIRST :LISTE |
| Ausgabe des n. Elementes |
ITEM n :LISTE |
| Einfügen eines neuen Elementes X in die Liste. Die neue Liste ist [X, A, B, C] |
MAKE "LISTE (FPUT "X, :LISTE) |
Tabelle 1b: Elementare Listenoperationen in LOGO
| Funktion |
Ausführung in PROLOG |
| Nimmt das Fakt, das [a, b, c] eine Liste ist in die Datenbank auf. |
assert(liste([a,b,c]). |
| Ausgabe des 1. Elementes der Liste in der Datenbank a |
liste([Erstes1]). |
| Ausgabe der Restliste [b, c] |
liste([... |
| Ausgabe des 2. Elementes b |
liste([...,Zweites |
| Ausgabe des n. Elementes |
liste(X),nth(n,X,Element).
mit: nth(1,[Kopf |
| Einfügen eines neuen Elementes x in die Liste in der Datenbasis. Die neue Liste ist [x, a, b, c] |
cons(x).
mit
cons(X):— liste(Y),assert(liste([X |
| Aneinanderfügen zweier Listen. Ergibt Liste = [a, b, c, d, e, f] |
append([a, b, c],[d, e, f], Liste). |
Tabelle 1c: Elementare Listenoperationen in PROLOG
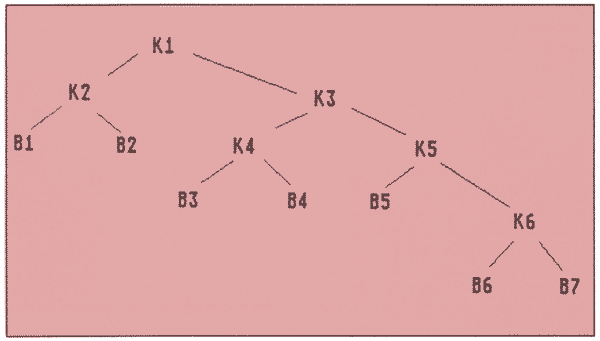 Abb. 1: Binärer Beispielbaum
Abb. 1: Binärer Beispielbaum
Evaluierung von LISP-Termen
Erfahrungsgemäß bereitet Anfängern die Evaluierung von LISP-Termen große Schwierigkeiten. Deshalb möchte ich die in Literaturliste 2 recht kurz geratene Einführung hier ergänzen. Generell versucht LISP (genauer gesagt ein eval-Lisp), den Wert eines Terms zu erfahren, bevor es ihn weiterverarbeitet. Zur Anschauung betrachte man den XLISP-Dialog in Abb. 2. In der ersten Zeile wird das Atom A an den Wert 1 gebunden. Da ein Atom (eine Zahl ist ein numerisches Atom) zu sich selbst evaluiert, ist in der Anweisung kein Apostroph für 1 erforderlich. Eigentlich müßte das Symbol A mit einem Apostroph eingegeben werden, um dem Interpreter zu verdeutlichen, daß das Symbol A als unevaluiertes Atom verwendet werden soll. Dies ist nicht erforderlich, weil meist eine Bindung ohnehin nur an ein Atom erfolgt und LISP deshalb vorsorglich das erste Argument mit einem Apostroph versieht, setq ist schließlich nichts anders als die Kurzform von set quote. (setq a 1) ist also äquivalent zu (set ’a 1). In der zweiten Anweisung wird schließlich das Atom B an die Liste (+ a 1) gebunden. Dies ist zwar die Anweisung, die Summe von a und 1 zu berechnen, da sie aber in der setq Anweisung quotiert wird, wird sie nicht ausgeführt. Wachsame haben vielleicht bemerkt, daß hier bereits die in Pascal, C, Basic & Co. streng durchgeführte Trennung von Programm und Daten verwischt. Hier dient eine Programmanweisung (addiere den Wert von a und 1) als Wert. Läßt man die Quotierung für das zweite Argument weg, dann wird die Evaluierung des zweiten Terms durchgeführt. D. h., die Summe von A und 1 wird erst berechnet und dann das Ergebnis an C gefunden (dritte Anweisung). Das Ergebnis der vierten Anweisung zu verstehen, dürfte nun keine Schwierigkeiten bereiten: A evaluiert zu 1. C evaluiert zu 2 und die Summe ist 3. Wer nun in der fünften Anweisung (+ a b) ein vernünftiges Ergebnis erwartet, hat zu hohe Erwartungen an den XLISP-Interpreter. Selbstverständlich evaluiert XLISP den Term zu ( +1 (+ A 1)). aber die Evaluierung wird nicht rekursiv bis zur letzten Stufe durchgeführt. sondern stoppt hier. Da die Addition zwei numerische Atome verknüpfen will, (+ A 1) aber eine Liste darstellt, ist nun die Fehlermeldung bad argument type zu erwarten. Sorgt man mit eval b jedoch ausdrücklich für eine Evaluierung des Termes 3. dann wird in der Tat die korrekte Summe ermittelt (sechste Anweisung):
(+ a (eval b)) — (+ a (+ a 1)) —
(+ 1 2) - 3
Einige einfache Anwendungen
Ungeachtet der Tatsache, daß LISP keine Sprache ist, in der man bevorzugt rechenintensive Vorgänge bearbeitet, betrachten wir als einfachstes Beispiel die Berechnung einer Wertetabelle. Dies läßt sich folgendermaßen erreichen:
(setq argumente ’(0.0 0.785398 1.04719 1.57079 3.14159))
(setq wertetabelle (mapcar sin argumente))
Diese zwei Zeilen berechnen den Sinus von 0,/4,ir/3,V2 und n . Die Funktionswerte findet man anschließend in der Wertetabelle wieder:
wertetabelle
(0.000000 0.707106 0.866021
1.000000 0.000020)
Ein weiteres einfaches Beispiel unter Verwendung der Listenfunktionen ist die Übersetzung eines deutschsprachigen Texten in pitching english. D. h., man übersetzt den Text wortweise und erhält ein mehr oder weniger brauchbares Konglomerat englischer Worte, die im Idealfall einen lesbaren Satz bilden. Dazu stellt man sich zunächst ein Lexikon in Form einer Assoziationsliste zusammen, deren erste Element jeweils das deutsche Wort und dessen zweites Element das zugehörige englische Wort darstellen. Dann läßt man die Assoziationsliste die entsprechenden Substitutionen durchführen und entfernt anschließend die störenden Klammern aus dem Text:
(setq deutsch_englisch '((dies this)
(satz sentence) (ein a) (ist is)) ((DIES THIS) (SATZ SENTENCE)
(EIN A) (IST IS))
(setq deutsch '(dies ist ein satz))
(DIES IST EIN SATZ)
(setq englisch (sublis deutsch_englisch
deutsch))
((THIS) (IS) (A) (SENTENCE))
(setq englisch (mapcar car englisch))
(THIS IS A SENTENCE)
Die letzten beiden Zeilen lassen sich natürlich noch zu einer zusammenfassen:
(DIES IST EIN SA TZ)
(setq englisch (mapcar car(sublis
deutsch__englisch deutsch)))
(THIS IS A SENTENCE)
Die eigentlich interessanten Anwendungen erhält man allerdings erst, wenn man seine eigenen Funktionen definieren kann. Dazu kommen wir aber erst in der nächsten Folge. Dann nämlich geht es um die Definition von Funktionen und das LAMBDA-Konzept. Wie Sie sehen, bleiben wir also noch ein wenig im LISP/LOGO-Sprachraum. Erst wenn wir die Prädikatsfunktionen besprechen, werden wir unseren Blick wieder stärker in Richtung PROLOG Lenken. Schließlich ist PROLOG die Sprache zur Verarbeitung logischer Prädikate.
[1] Sarnow, K. Einführung in die künstliche Intelligenz. ST-Computer 11/86.
[2] Sarnow, K. XLISP Review. ST-Computer 1/87
[3] Sarnow, K. TOY-PROLOG Review. ST-Computer 2/87.
[4] Wirth, Niklaus. Algorithmen und Datenstrukturen. B. G. Teubner, 1975.
append
: Siehe Tabelle 1a.
assoc
: Findet einen Term in einer Assoziationsliste. Beispiel:
(setq arbeiter ’((name emil) (gehalt 1526.65)))
(assoc ’gehalt arbeiter)
(GEHA L T 1526.650000)
car
: Siehe Tabelle 1a.
cdr
: Siehe Tabelle 1a.
cxxr
: xx bedeutet eine beliebige Kombination von a und d. z. B. cadr oder cdar oder cddr oder caar. Siehe Tabelle 1a.
cxxxr
: Siehe cxxr und Tabelle 1a.
cxxxxr
: Siehe cxxr und Tabelle 1a.
cons
: Siehe Tabelle 1a.
last
: Ergibt die Liste, welches das letzte Element enthält. Beispiel:
(last ’(a b c))
(c)
length
: Gibt als Funktionswert die Anzahl der in der Liste enthaltenen Elemente an. Beispiel:
(length ’(a b (c d)))
3
list
: Der Funktionswert ist eine Liste der Argumente. Beispiel:
(list ’a ’b ’(c d))
(a b (c d))
mapc
: Wendet die Funktion (1. Argument) nacheinander auf die Listen der Argumentwerte (2. - n. Argument, eine Liste je Argument der Funktion) an. Als Funktionwert wird die erste Liste von Argumenten ausgegeben (2. Argument von mapc). Beispiel:
(mapc + ’(1 2 3) ’(4 5 6)))
(1 2 3)
Man beachte, daß von der Summation nichts bemerkt wird, da die Funktion + (Addition) nebeneffektfrei ist und die Ergebnisse einfach vergessen werden. Diese Listenfunktion sollte deshalb nur bei Funktionen mit Nebeneffekt angewendet werden. Beispiel:
(mapc (lambda (x y) (prinl (+ x y))) ’(1 2 3) ’(4 5 6))
579(1 2 3)
Uber die Bedeutung von lambda später.
mapcar
: Wie mapc, allerdings wird hier als Funktionswert die Liste der Funktionswerte zurückgegeben. Beispiel:
(mapcar + ’(1 2 3) ’(4 5 6))
(5 7 9)
mapl
: Wie mapc, wendet die Funktion aber auf die cdr der Argumentlisten an. Beispiel:
(mapl length ’(a b c))
(a b c)
Man beachte auch hier, daß die Funktion Nebeneffekte haben muß, um eine Wirkung zu zeigen.
maplist
: Wie mapcar, wendet die Funktion aber au die cdr der Argumentlisten an. Beispiel:
(maplist length ’(a b c))
(3 2 1)
Zuerst ist die Argumentliste (a b c) und deren Länge 3. Der cdr dieser Liste ist (b c), die Länge 2. Der cdr dieser Liste ist (c), die Länge 1. Dann bricht maplist ab, weil der folgende cdr NIL ist.
member
: Findet einen Ausdruck in einer Liste und gibt die Restliste zurück. Beispiel:
(member ’b ’(a b c))
(b c)
nth
: Siehe Tabelle 1a.
nthcdr
: Gibt den n-ten cdr einer Liste zurück. N = 0 ergibt die Originallfte. Beispiel:
(nthcdr 2 ’(a b c d e f))
(c d e f)
remove
: Entfernt einen Term aus einer Liste. Beispiel:
(remove ’b ’(a b c))
(a c)
reverse
: Kehrt eine Liste in der Reihenfolge ihrer Elemente um. Beispiel:
(reverse ’(a b c))
(c b a)
sublis
: Ersetze mit Hilfe einer Assoziationsliste. Beispiel:
(sublis ’((halli hallo)) '(aber halb))
(ABER (HALLO))
subst
: Ersetzt LISP Terme. Beispiel:
(subst ’demo ’b ’(a b c))
(a demo c)
Tabelle 2a: Listenfunktionen in XLISP
delete
: Löscht einen Term aus einer Liste. Beispiel:
(setq liste ’(a b c))
(A B C)
(delete liste ’b)
(A C)
nonc
: Vereinigt zwei Listen zu einer (physisch). Beispiel:
(setq liste 1 ’(a b c))
(A B C)
(setq liste2 ’(d e f))
(D E F)
(nonc liste 1 liste2)
(A B C D E F)
liste 1
(A B C D E F)
liste 2
(D E F)
rplaca
: Ersetzt den car einer Liste. Beispiel:
(setq liste ’(a b c))
(A B C)
(rplaca liste ’b)
(B B C) liste
(B B C)
rplacd
: Ersetzt den cdr einer Liste. Beispiel:
(setq liste ’(a b c))
(A B C)
(rplacd liste ’(d e))
(A D E) liste
(A D E)
Tabelle 2b: Listenprozeduren in XLISP (destruktiv)
> (setq a 1) <-------------------A wird an den Wert 1 gebunden
1
> (setq b ’(+ a 1)) <-----------B wird an die Liste (+ A 1) gebunden
(+A 1)
> (setq c (+ a 1)) <------------C wird an den Wert der evaluierten
2 Liste (+ A 1) gebunden, d. h. an 2.
> (+ ac) >----------------------A evaluiert zu 1 C evaluiert zu 2,
3 die Summe beider ergibt 3.
> (+ a b)
error: bad argumenttype - (+ A1) B evaluiert zu - AI), das ist der
1: > falsche Argumenttyp für eine Addition.
> (+ a (eval b)) >--------------Eval be. = _o zu (+ A1), dies wird
3 zu 2 evaluiert. A wird zu 1 evaluiert,
> die Summe ergibt 3.
Abb. 2: Protokoll eines XLISP Dialoges zum Problem der Evaluierung