
Heute möchte ich Ihnen eine Verfeinerung der Baumstruktur vom letzten Mal vorstellen, die AVL-Bäume. Benannt nach ihren Erfindern, den Herren Adelson-Velskii und Landis, beheben Sie ein großes Manko, welches botanische und informatische Bäume immer besitzen: 'Sie wachsen wild!'
Sinn und Nutzen der AVL-Bäume
Dazu betrachten wir einige mögliche Bäume, die durch das Einfügen von sieben Elementen in die Baumstruktur vom letzten Mal entstehen können.
Wie Sie in Abbildung 5a leicht erkennen, sieht, in Abhängigkeit von der Eingabereihenfolge, das Aussehen der resultierenden Bäume sehr unterschiedlich aus. Bei der linken Eingabesequenz sehen Sie, daß der Baum zu einer linearen Liste wird. Dabei geht der große Vorteil der Suchbäume, die kurzen Suchwege, verloren. Deshalb nennt man diesen Baum und andere Bäume, denen man die Baumstruktur nicht mehr ansehen kann, degenerierte Bäume.
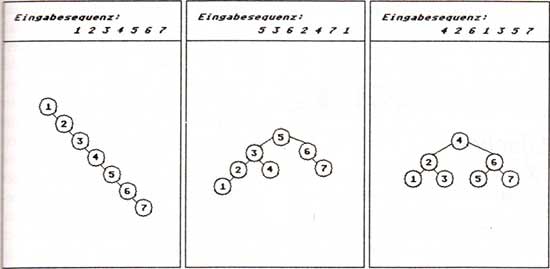 Bild 5a: Von degenerierten, vollständig und nur ein "bißchen" angeglichenen Bäumen
Bild 5a: Von degenerierten, vollständig und nur ein "bißchen" angeglichenen Bäumen
Die Aufgabenstellung ist es nun, eine Möglichkeit zu finden, nach Ein- und Ausfügen in Bäumen, durch Ausgleichsmechanismen, wieder kurze Suchwege zu erreichen, also die Degenerierung von Bäumen zu verhindern. Dabei ist der rechts in Abbildung 5a dargestellte Idealzustand, in der Regel, nur mit großem Aufwand herzustellen. Deshalb benötigen wir zunächst eine etwas schwächere Definition der Ausgeglichenheit, die effektive Algorithmen erlaubt. Dazu betrachten wir eine Definition für einen ausgeglichenen Baum, die auf die, schon erwähnten, Herren A.V.L. zurückgeht:
Ein Baum wird genau dann als 'ausgeglichen' bezeichnet, wenn für alle seine Knoten gilt, daß sich die Höhen des linken und des rechten Teilbaumes um nicht mehr als eins unterscheiden.
Betrachtet man, mit Augenmerk auf diese Definition, die Bäume der Abbildung 5a, ist klar: Der rechts dargestellten Idealzustand, auch als vollständig ausgeglichen bezeichnet, ist ein AVL-Baum. Aber auch schon der mittlere Baum gibt sich, nach kurzem Hinschauen, als AVL-Baum zu erkennen. Gerade dieser kleine Spielraum, zwischen ausgeglichen und vollständig ausgeglichen, macht die Anzahl der, nach Ein- und Ausfügen in Bäumen, notwendigen Ausgleichsvorgänge, beim AVL-Verfahren, vertretbar.
Balance-Faktoren
Bevor wir uns nun an die einzelnen Mechanismen machen, möchte ich kurz auf die Höhenermittlung der Teilbäume eingehen. Wie Sie sicherlich leicht einsehen, ist es völlig unwirtschaftlich, nach jeder Operation, die die Baumstruktur verändert, die Länge sämtlicher Teilbäume zu ermitteln. Statt dessen bietet es sich an in die Baumstruktur, speziell in jedem Baumelement, einen zusätzlichen Merker einzubauen, der die Höhendifferenz des rechten und des linken Teilbaums verzeichnet. Da wir es mit AVL-Bäumen zu tun haben, hat dieser Merker nur drei mögliche Werte:
-1 : Der linke Teilbaum ist um eins höher.
0 : Beide Teilbäume sind gleichhoch.
+1 : Der rechte Teilbaum ist um eins höher.
Diesen Merker, bal genannt, werde ich zusätzlich in die b_element-Definition der letzten Folge aufnehmen. Zusammen mit den, an unsere heutige Anwendung - eine Adreßdatei - angelehnten Schlüßel- und Datentypdefinitionen, ergeben sich die Typen des Listings 5a.
An den Operationen der letzten Folge bewirken diese Vereinbarungen folgende Änderungen:
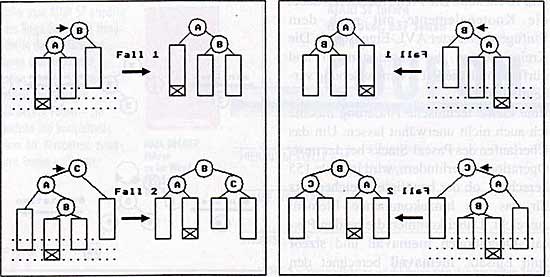 Bild 5b: Vier Ausgleichssituationen beim Einfügen und ihre Symmetrie
Bild 5b: Vier Ausgleichssituationen beim Einfügen und ihre Symmetrie
Einfügen
Das Einfügen in AVL-Bäume unterscheidet sich zunächst in keiner Weise von dem Einfügen in einfache binäre Bäume. Auch hier muß, über die rekursive Baumsuche, der Suchpfad bis zur Einfügestelle ermittelt werden. Nach dem Einfügen, ist aber zusätzlich die Höhenänderung zu berücksichtigen. Dazu wird in die Parameterliste, der Funktion put_in (rekursive Subprozedur von insert), zusätzlich ein bool'scher Parameter h aufgenommen, der wahr wird, wenn eine Höhenänderung stattgefunden hat, falsch, sonst.
Anmerkung: Nach dem Einfügen ist h zunächst immer wahr, weil auf jeden Fall eine Balancefaktoränderung des Vaterknotens der Einfügestelle auftritt.
Der rekursive Charakter von put_in kommt uns nun sehr zu statten. Wir müssen nur nach dem rekursiven Aufruf von put_in eine Abfrage auf eine Höhenänderung starten. Hat eine Höhenänderung stattgefunden, so bestehen prinzipiell drei Möglichkeiten:
- Die Höhenänderung eines Teilbaumes gleicht ein, zuvor beste hendes, Ungleichgewicht des AVL-Baumes aus. In diesem Fall wird der Balancefaktor '0' und in den höher liegenden Knoten findet keine Höhenveränderung mehr statt, h ist also auf 'false' zu setzen.
- Die Höhenänderung trifft bei einem Knoten mit gleich hohen Teilbäumen ein. Hier findet eine Balancefaktoränderung im Rahmen der AVL-Eigenschaft statt. Der Balancefaktor wechselt von '0' zu '-1', oder '+1', je nachdem, in welchem Teilbaum eingefügt wurde. Diese Änderung bewirkt nun aber auch eine Änderung der Teilbaumhöhe des nächst höheren Knotens.
h ist also auf dem Wert 'true' zu belassen.
- Die Höhenänderung verletzt die AVL-Eigenschaft. In diesem Fall sind Ausgleichsoperationen auszuführen.
Nach gründlicher Überlegung kommt man - die Herren A.V.L. und nach einiger (!) Zeit auch ich - zu dem Ergebnis, daß sich, bis auf Symmetrie, nur zwei mögliche Ausgleichssituationen ergeben können. Diese beiden Situationen, und die symmetrischen Situationen, sind in der Abbildung 5b dargestellt. Entsprechend den Bewegungen, der an den Rotationen beteiligten Knoten, A-C, nennt man:
Fall 1a eine L-Rotation,
Fall 1b eine R-Rotation,
Fall 2a eine LR-Rotation,
Fall 2b eine RL-Rotation,
wobei L für Links- und R für Rechts-Rotationen steht.
Die gestrichelten Linien verdeutlichen sehr schön, wie die Teilbäume, die die AVL-Eigenschaft verletzen, bei den entsprechenden Rotationen angehoben werden.
Im Listing findet man die Zeigerrotationen für L in den Zeilen 77-80, für LR in 84-97, für R in 119-122 und für RL in 126-139.
Bemerkenswert ist dabei, daß durch lediglich eine (!) Rotation die AVL-Eigenschaft wieder hergestellt wird. Bei der AVL-Löschoperation werden wir damit, im Regelfall, nicht auskommen. Doch zuvor noch ein kleines Beispiel zum Einfügen. Betrachten Sie die Abbildung 5c. Hier dargestellt ist der AVL-Baum, der durch Einfügen der Elemente 9, 1, 3, 5, 4 und 10 entsteht. Die Pfeile markieren dabei die Knotenelemente mit, nach dem Einfügen, verletzter AVL-Eigenschaft. Die Kreise deuten die Rotationen an und dürften somit die R-L-Namensgebung verdeutlichen.
Eine kleine technische Änderung möchte ich auch nicht unerwähnt lassen. Um das Überlaufen, des Pascal-Stacks bei der new-Operation zu verhindern, wird in Zeile 155 berechnet, ob der benötigte Speicherplatz für das neu hinzukommende Element ausreicht. Dabei kommen die beiden Pascal+ Operationen memavail und sizeof zum Einsatz. memavail berechnet den verfügbaren Speicher in Worten; sizeof das Format des übergebenen Typs in Byte. Ist der Speicher (store) ausreichend, wird das Element eingefügt. Der bool'sche Rückgabeparameter von insert bekommt den Erfolg, dieser Aktion, zugewiesen.
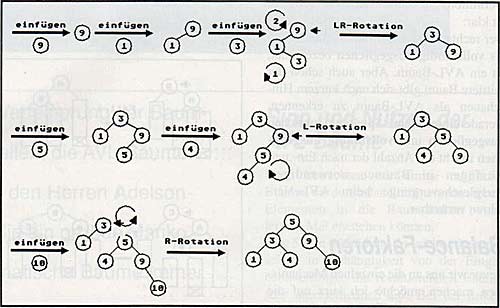 Bild 5c: Einfügen an einem Beispiel
Bild 5c: Einfügen an einem Beispiel
Löschen
Auch die Löschoperation gestaltet sich nicht prinzipiell anders, als in der letzten Folge. Hier erfolgt ebenfalls zunächst die rekursive Baumsuche (in delete). Zusätzlich zur letzten Folge, ist hier, wie schon bei insert, eine bool'sche Hilfsvariable h mit in die Parameterliste aufgenommen worden. Diese zeigt jetzt allerdings eine Höhenminderung an.
Das Ausfügen des Knotens selber gliedert sich wieder in drei Fälle:
- Kein rechter Nachfolger
- Kein linker Nachfolger
- Zwei echte Nachfolger
Für den nicht-trivialen letzten Fall, ist diesmal, abweichend zur letzten Folge, eine rekursive Ausfügeprozedur (del) angegeben. Die Zeigerrotation (balance1 und balance2), mit Aussehen ähnlich den Rotationen beim Einfügen, sind diesmal, um redundanten Code zu vermeiden, als Prozedur formuliert. Ansonsten realisieren sie die gleichen Aufgaben, wie die Rotationen in insert. Der entscheidende Unterschied ist, daß beim Löschen eventuell mehr als eine Ausgleichsoperation durchgeführt werden muß.
Eine weitere Änderung gegenüber dem letzten Mal, ist die Behandlung eines, oder mehrerer, Elemente, die ausgefügt werden sollen. Wurden sie bei letzten Mal lediglich aus dem Baum ausgeklinkt, so wird diesmal, über die Variable del_list in der Parameterliste von remove, ein Zeiger auf die ausgefügte Elementliste übergeben. Dadurch besteht nun die Möglichkeit, entweder, durch die aufrufende Programmstelle, die Speicherfreigabe der Elementnachfolgerliste zu betreiben, oder mit dieser Liste eine Sicherheitsabfrage zu durchlaufen, in der einzelne, oder alle, Listenbestandteile wieder in den Baum eingefügt werden können. Wie diese letzte Möglichkeit zu handhaben ist, wird sich noch in unserer heutigen Anwendung zeigen.
Andere AVL-Operationen
Die anderen AVL-Operationen unterscheiden sich nicht wesentlich von den Operationen der letzten Folge. Um die Fehleranfälligkeit der Dateioperationen zu senken, sind diese jedoch mit einem IO-Laufzeitcheck versehen worden. Dazu sind im Kopf des Listing 5b die beiden externen Pascal+ Operationen io_check und io_result vereinbart worden. Mit io_check(false) wird, vor Beginn des Datenzugriffs auf Datei, der IO-Check abgeschaltet. Dies bewirkt, daß sich Pascal+ nicht bei jedem kleinen IO-Fehler verabschiedet und, im Anschluß an einen Dateizugriff, die Fehlerkennung, mit io_result, erfragt werden kann. Entsprechend der Möglichkeit eines fehlerhaften Dateizugriffs, wurden die beiden dazu vorgesehenen AVL-Operationen, load und save, als Funktionen mit bool'schem Rückgabewert deklariert.
Von indizierten und sequentiellen Zugriffen
Ohne sie beim Namen genannt zu haben, wurden in der heutigen und in der letzten Folge bereits die zwei Arten von Zugriffen auf eine Datenbank behandelt. Es handelt sich dabei um:
A: Indizierte Zugriffe, die schnell über irgendeine Organisationsstruktur (Index) erfolgen (Binärbaum, AVL-Baum, ...).
B: Sequentielle Zugriffe, die die kompletten Daten durcharbeiten und dabei mitunter recht langsam sind. Bei den Baumstrukturen sind dies die X-order-Zugriffe.
Mit einer besonderen, sequentiellen Form des Auffindens von Daten, möchte ich mich nun befassen.
Ausgangspunkt ist dabei die Idee einer Adreßdatei, als Anwendungsbeispiel für Bäume. Da in so einer Adreßdatei sämtliche Daten in Form von Strings gespeichert werden können, werden wir nun eine Möglichkeit behandeln, Daten zu finden, indem wir ein Suchmuster für die entsprechenden Daten vorgeben und während eines X-order-Durchlaufs dieses Suchmuster mit sämtlichen Datensätzen vergleichen. Mächtigkeit erlangt dieses Konzept durch die Möglichkeit Wildcards ('*' und '?') bei den Suchmustern zu verwenden.
Beispiel: Vorausgesetzt die Typdefinitionen für unsere Adreßdatei, möchten wir uns sämtliche Dortmunder, die Peter heißen und in unserer Adreßdatei gespeichert sind, ausgeben lassen. Als Suchmuster geben wir also vor:
Anrede : *
Vorname : *Peter*
Nachname : *
Strasse : *
Wohnort : *Dortmund*
Telefon : *
Eine Stringrelation
Was nun benötigt wird, um Datensätze mit derartigen Suchmustern vergleichen zu können, ist im Wesentlichen eine Stringrelation, die Wildcards berücksichtigt (Listing 5c, Zeilen 54-107).
Dabei gehen wir davon aus, daß einer der beiden Strings Wildcards enthalten darf, der Andere nicht. Beim Vergleich der beiden Strings wird nun versucht, beide, bis auf den leeren String ('') zu reduzieren, indem gleiche Buchstaben abgetrennt werden und mit den Reststrings ein rekursiver Aufruf der Stringrelation erfolgt. Wurde nun, in irgendeinem Teil des rekursiven Aufrufbaumes der Prozedur, eine Reduktion auf zwei leere Strings erzielt, so ist ein Flag zu setzen, das, zum einen den Abbruch der Rekursion veranlaßt, und, zum anderen als Gleichheitsbit dient (equal).
Beispiel: norm_str = 'abcde' wild_str = 'ab?*'
Der rekursive Aufrufbaum hätte folgendes Aussehen:
durchlauf('ab?*','abcde')
durchlauf('b?*','bcde')
durchlauf('?*','cde')
durchlauf('*','de')
durchlauf('','e') und durchlauf('','')
Hierbei führt der zweite Teil, des durch '*' verursachten Doppelaufrufs, zu einer Auslöschung der beiden Strings, also zur Vergleichbarkeit der ursprünglichen Strings.
muster_inorder
Zum sequentiellen Durchlauf der Baumstruktur, habe ich den inorder-Durchlauf (Zeilen 109-132) gewählt. Zusätzlich zu den beiden Teilbäumen ist dabei noch die Nachfolgerliste zu durchlaufen (ebenfalls rekursiv). Auf den Knoten wird, in inorder-Position, die Stringrelation auf sämtlichen Schlüßel- und Datenstrings ausgeführt. Dabei werden die entsprechenden Knoteninhalte mit den Werten einer globalen Variable muster verglichen. Bei der Variable muster handelt es sich um einen b_file_type, da die Organisationsvariablen für die Baumstruktur weder bei den Dateioperationen, noch bei den Suchmustern benötigt werden.
Als Operation, die in die Rekursion eingeschachtelt ist, habe ich eine Elementausgabe gewählt. Denkbar sind natürlich alle möglichen Operationen, denen lediglich gemeinsam ist, daß sie die Baumstruktur festhalten. Also beispielsweise 'Editieren des Datensatzes'. Dabei ist allerdings darauf zu achten, daß der Schlüßel nicht verändert wird, denn sonst geht die Ordnung der Baumstruktur verloren.
eingabe und ausgabe
Zwei Operationen, die ebenfalls nicht fehlen dürfen sind die beiden Operationen eingabe und ausgabe zum Lesen und Schreiben eines Datensatzes. (eingabe wird auch zur Mustereingabe verwendet.)
main
Das Hauptprogramm beinhaltet nun, organisiert in einem zentralen CASE-Statement, die sieben Operationen, Eingabe, Löschen, Suche nach Muster, Suche nach Nachname, Speichern, Laden und Löschen.
Einen etwas mehr als trivialen Operationsaufruf, bieten aber nur die beiden Operationen Löschen und Suche nach Nachname.
Bei Löschen (CASE-Label 2) wird, nach dem Ausfügen aus dem Baum, die dabei ausgefügte Elementenliste durchlaufen. Die Datensätze, die dabei als wertvoll erachtet werden, werden erneut in die Baumstruktur eingefügt, die Anderen werden freigegeben.
Bei der Suche nach Nachnamen (CASE-Label 4) ist, nach dem Auffinden eines Elementes mit search_first, die Elementnachfolgerliste, mit search_next, zu durchlaufen.
Vorausschau
In der nächsten Folge werde ich Sie mit einem etwas anderen Ansatz zur Suchpfadoptimierung in Bäumen bekannt machen, den sogenannten B-Bäumen.
Denjenigen unter Ihnen, denen die Botanik langsam zum Hals heraushängt, sei versichert, daß es sich dabei um den letzten Vertreter der Spezies Baum handeln wird.
Listings zu diesem Artikel