Seit einiger Zeit verfügt so ziemlich jedes gute Vektorgrafikprogramm über die Fähigkeit, zu arbeiten. wer sich schon einmal mit dem Verfahren, mit dem Bézier-Kurven auf mathematischem Wege berechnet werden, beschäftigte, wird sich fragen, wie programme wie Calamus, LineArt etc. diese so schnell berechnen.
Mathematisch gesehen läßt sich die Bézier-Kurve „durch ein Polynom n-ten Gerades bei n+1 gegebenen Führungspunkten berechnen“ (Wortlaut aus [1 ]). Würde man dieses Verfahren in einem DTP-Programm anwenden bräuchte man schon eine etwas schnellere FPU, um die Nerven des Anwenders nicht überzustrapazieren. Man könnte dieses Polynom auch mit Pseudo-Floats in Form von Longlnts (je 16 Bit Vor- und Nachkommateil) ausmultiplizieren - gegenüber dem ersten Verfahren ergäbe sich eine erhebliche Geschwindigkeitssteigerung - in Anbetracht der Geschwindigkeit der Multiplikationsoperationen des 68000-Prozessors (<70 Taktzyklen für Ints) ist dies jedoch weniger akzeptabel (Es hat halt nicht jeder einen 68030).
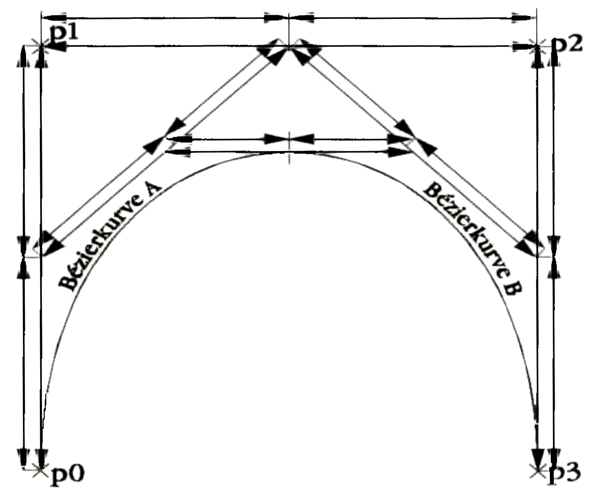
Betrachtet man sich in Programmen wie Outline Art eine Bézier-Kurve in der Vergrößerung, so ist festzustellen, daß diese in mehrere Linien unterteilt ist. Die Anzahl der Linien ist immer eine Zweierpotenz, was wohl, wie sich heraussteilen wird, weniger ein Zufall ist. Die Bézier-Kurve läßt sich nämlich durch ein einfaches baumstrukturartiges Halbierungsverfahren, also vorzugsweiserekursiv, „berechnen“ (es gibt nichts Schöneres als Re-kursionen und binäre Bäume). Man kann sie auch iterativ berechnen, was jedoch um einiges langsamer und weniger elegant ist.
Der hier vorgestellte Algorithmus arbeitet wie in Abb. 1 beschrieben. Er erwartet nach Turbo-C-Konvention zwei Pointer (a0, a1) und einen int-Parameter (d0), der die Rekursionstiefe und somit die Anzahl der berechneten Punkte auf der Bézier-Kurve angibt. Die zwei Pointer zeigen jeweils auf die vier vorzeichenbehafteten x- und y-Komponenten (int-Werte, d.h. -32768 - +32767) der Koordinaten. Die Anzahl der berechneten Punkte ist 1 +2A(n+l), wobei n die Rekursionstiefeist. Falls benötigt, läßt sich diese Anzahl dem Rückgabewert der Funktion entnehmen.
Arbeitsweise
Intern wird mit den schon oben erwähnten Pseudo-Floats gearbeitet, d.h. jeweis 16 Bit für Vor- und Nachkommateil (keine BCD-Kodierung). Der Nachkommateil wird am Anfang nicht mit Nullen aufge-füllt, sondern mit $8000, d.h. es wird z.B. nicht auf der x-Koordinate 10.012.0 gerechnet, sondern auf 10.512.5, dem eigentlichen Pixel-Mittelpunkt (wird häufig vergessen). Die eigentliche Rekursionsroutine ist sehr klein, so daß sie komplett in den Instruction-Cache des TTs paßt (bzw. passen würde). Es werden zuerst alle x-, dann alle y-Komponenten der Stützpunkte errechnet.
Da das hier beschriebene Verfahren auf einem einfachen Halbierungsverfahren basiert, läßt sich mit dementsprechend einfachen shift-Operationen arbeiten. Folgende Situation sei gegeben: In Register A und B befinden sich zwei vorzeichenbehaftete (!) int-Werte, deren Arithmetisches Mittel errechnet werden soll. Register B darf hierbei zerstört werden. Um dies zu bewerkstelligen, sind folgende Operationen nötig:
add.w Da,Db asr.w #1 ,Db
Angenommen, beide Werte seien negativ, das MSB sei also gesetzt. Bei der Addition würde das Vorzeichen-Bit im X-Flag des Statusregisters landen, was bei dieser Methode jedoch nicht berücksichtigt wird. Um auch vorzeichenbehaftete Werte in jedem Fall richtig zu mit-teln, benutzt man besser die folgende Sequenz:
add.w #$8000,Da
add.w #$8000,Db
add.w Da.Db
roxr.w #1,Db
sub.w #$8000,Da
sub.w #$8000,Db
Durch das Addieren der Konstante $8000 werden beide Werte vom 2-Komplement ins vorzeichenlose Format gewandelt, d.h. um 32768 (=$8000) verschoben. Dadurch, daß unter Berücksichtigung des X-Flags geshiftet wird, wird ein eventueller arithmetischer Über] auf der Addition abgefangen. Anschließend werden beide Werte wieder durch das S ub-trahieren der Konstante $8000 (in der Routine als Registerkonstante) zurückgeschoben. Die hier beschriebene Routine rechnet so lange mit dem vorzeichenlosen Format, bis eine Komponente einer Koordinate ins Koordinatenfeld eingetragen werden muß. Dies hat nur eine unwesentliche Auswirkung auf die Geschwindigkeit.
In der Rekursion wird zuerst die Bézier-Kurve in zwei Teile geteilt. Darauf wird der Zähler für die Rekursionstiefe (d7) dekrementiert. Hat dieser den Wert -1 erreicht (Carry set), so werden die auf der Kurve liegenden Koordinaten gesetzt. Ansonsten geht’s eine Rekursionsebene tiefer. Böse Überraschungen kann es geben, wenn der Stack zu klein ist und somit ins data- oder sogar ins code-Segment läuft. Pro Rekursionsebene werden nämlich 18 Byte Stack gebraucht.
Literatur:
[1] Kai Hendrik Komp: Bézier-Kur-ven, ST-Computer 5/91
[2] Foley, Van Dam: Fundamentals of Interactive Computer Graphics, Addison Wesley, 1984
; ***********************************************
; * Fast-Bézier-Routine *
; * von Oliver Schädlich *
; * (c) 1992 MAXON Computer *
; * *
; * deklaration in TC: *
; * extern int f_bezier( int *xvals, *
; * int *yvals, int rec count ); *
; * *
; ***********************************************
.GLOBL f_bezier
f_bezier:
movem.l d3-d7/a2,-(sp) ; Register retten
move.w d0,d7 ; Rekursionszähler -> d7
movea.w #$8000,a2 ; n.5, um aufm Pixel-Mittelpunkt zu rechnen
bsr init_rec ; =>x-Kurvenpunkte errechnen
movea.l a1,a0 ; =>y-Kurvenpunkte errechnen
bsr init_rec
moveq #2,d0 ; Anzahl der Punkte -> d0
lsl.w d7,d0
addq.w #1,d0
movem.l (sp)+,d3-d7/a2 ; Register restaurieren
rts ; zurück
init_rec:
move.w (a0)+,d0 ; n0 -> d0
movem.w (a0),d1/d5/d6 ; n1...n3 -> dl/d5/d6
add.w a2,d0 ; n0...n3 ins
add.w a2,d1 ; unsigned-Format
add.w a2,d5 ; wandlen
add.w a2,d6
swap d0 ; Werte ins high-word
swap d1 ; und Machkommastelle
swap d5 ; (n.5) anhängen
swap d6
move.w a2,d0
move.w a2,d1
move.w a2,d5
move.w a2,d6
fb_rec: ; Bézier-Rekursion
move.l d5,d2 ; (nl + n2) / 2 -> d2
add.l d1,d2
roxr.l #1,d2
add.l d0,d1 ; n1.0 -> d1
roxr.l #1,d1
add.l d6,d5 ; n2.1 -> d5
roxr.l #1,d5
move.l d5,d4 ; n1.1 -> d4
add.1 d2,d4
roxr.l #1,d4
add.l d1,d2 ; n2.1 -> d2
roxr.l #1,d2
move.l d4,d3 ; n0.1 -> d3
add.1 d2,d3
roxr.l #1,d3
subq.w #1,d7 ; Rek.- Zähler dekrementieren
bcc rcall_x ; >=0: =>nächste Rek.-Ebene
set_n:
swap d3 ; n3.0
sub.w a2,d3 ; zurück ins signed-Format
move.w d3,(a0)+ ; und setzen
swap d6 ; n3.1
sub.w a2,d6 ; zurück ins signed-Format
move.w d6,(a0}+ ; und setzen
addq.w #1,d7 ; Rek.-Zähler Inkrementieren
rts ; <=zurück
rcall_x:
movem.l d3-d6,-(sp) ; 1. Bézierhälfte auf'n Stack
rcall_left:
move.l d2,d5 ; richrige Reg.-konstellation
move.l d3,d6 ; für nächste Rek.-Ebene
bsr fb_rec ; =>nächst tiefere Rek.-Ebene
rcall_right:
movem.l (sp)+,d0/d1/d5/d6 ; r. Bézierhälfte zurück
; und automatisch richtige
; Reg.-Konstellation für
; nächste Rek.-Ebene
bsr fb_rec ; =>nächst tiefere Rek.-Ebene
addq.w #1,d7 ; Rek.-Zähler inkrementieren
rts ; <=zurück